반응형
발칙한 MIT 천재들의 라스베가스 무너뜨리기라는 흥미로운 소재를 영화화한 <21>. MIT 졸업과 동시에 하버드 의대 입학을 앞둔 수학천재 벤 캠벨. 그의 뛰어난 수학능력을 탐내는 미키 교수는 비밀리에 활동하는
MIT 블랙잭 팀에 가입할 것을 권유합니다. 30만 달러의 등록금이 절실히 필요했던 벤은 결국 유혹을 거절하지 못하고 팀에 가입하게 되고, 미키 교수의 지도 아래 카드 카운팅 기술 등을 익혀 주말마다 라스베가스에서 블랙잭 게임으로 어마어마한 돈을 벌어들이게 됩니다.

영화의 기본 소재가 되는 MIT 수학 천재들의 라스베가스 원정기는 놀랍게도 1990년대 확률과 수학만으로 블랙잭의 법칙을 간파해 라스베가스를 제패한 '제프 마'의 실화에 바탕하고 있습니다. 이런 천재들의 실화에 바탕한 영화들을 볼 때면 '언젠가는 나도 저 천재들처럼 크게 한 탕...!!'이 아니고...-_-; 천재라 불리우는 사람들의 삶의 단면을 엿보는 듯한 즐거움을 느낄 수 있어 즐겨보곤 합니다. 이런 유형의 작품으로는 게임이론의 대가 '존 내쉬'의 이야기를 영화화한 '뷰티풀 마인드(Beautiful Mind)'가 있겠죠. '뷰티풀 마인드' 역시 참 재미있게 봤었는데, 예전에 봤던 영화라서 아직까지 후기를 못 쓰고 있네요. 언젠간 작성해야 하는데...^^;
아무튼 오늘의 포스팅은 영화 <21>에 대한 리뷰가 아니라 영화 <21>을 좀 더 편안하게 즐기기 위해 감상하기 전에 미리 알아두면 좋을 것 같은 포인트 하나를 알려드리기 위한 것입니다. 리뷰는 나중에 언젠가...-_- 혹시라도 영화를 봐야 하나, 말아야 하나 고민하고 계시는 분들을 위해 살짝 말씀드리자면...재밌습니다.

앞에서도 말씀드린 것처럼 미키 교수는 벤을 자신의 블랙잭 팀에 가입시키기 위해 꽤나 열심히 노력합니다. 미키 교수가 벤에게 호감을 가지기 시작한 시점은 바로 자신의 강의를 듣고 있던 벤의 뛰어난 수학 및 통계학 실력을 발견하고 나면서부터입니다.
강의 시간에 미키 교수가 '뉴턴의 공식'과 관련해 자신이 모르는 얘기를 좀 해 달라고 학생들에게 주문하자, 벤이 '뉴턴이 조셉 랩슨의 공식을 훔쳤다'라는 답변을 합니다. 벤의 답변에 흥미를 느낀 미키 교수는 벤에게 추가 점수를 얻을 수 있는 기회를 주겠다며 '게임 진행자의 문제'를 냅니다.
미키 교수가 제안한 '게임 진행자의 문제'
미키 교수가 제안한 '게임 진행자의 문제'는 다음과 같습니다. 벤이 게임쇼에 출연했다고 가정을 합니다. 세 개의 문 중에서 하나를 고르면 되는데, 한 개의 문 뒤에는 새로운 자동차가 기다리고 있고 나머지 두 개의 문 뒤에는 염소가 기다리고 있습니다. 이 중에서 새로운 자동차가 숨어 있는 문을 고르면 그 자동차를 선물로 얻을 수 있는 그런 게임입니다. 벤에게 어떤 문을 고르겠냐고 물어보는 미키 교수. 벤은 망설임없이 1번 문을 선택합니다.
벤의 선택을 듣고 난 교수는 추가적으로 새로운 정보를 제시합니다. 게임을 진행하는 사회자는 문 뒤에 무엇이 있는지 정확히 알고 있습니다. 그래서 벤이 고르지 않은 두 개의 문 중에서 하나의 문을 열어 제꼈더니 그 문 뒤에는 염소가 있었습니다. 일부러 염소가 숨어 있던 문을 선택해 열어준 것이죠.
이제 사회자는 벤에게 다가와 다시 한 번 선택을 하도록 제안합니다. 처음 선택한 1번 문을 그대로 선택할 것인지, 아니면 다른 문으로 바꿀 것인지 말이죠. 교수의 새로운 질문에 대해 벤은 또 다시 주저하지 않고 '바꾸겠다'라고 답을 합니다. 심리적인 문제에 근거한 것이 아니라 통계학에 근거하여 답한 것이라 설명하면서요. 벤이 선택을 바꾼 이유를 논리적으로 설명하고 나자 미키 교수는 벤에게 완전히 빠져들고, 벤을 자신의 블랙잭 팀에 가입시켜야겠다고 결심하게 됩니다.
자, 그런데 벤이 1번 문에서 다른 문으로 선택을 바꾼 것은 정말 통계학에 근거한 것일까요? 얼핏 생각하면 한 개의 문은 이미 꽝인 것으로 판명되었고, 나머지 두 개의 문 중에서 1개를 선택하는 것이므로 자신이 선택했던 1번 문을 그대로 선택하든, 다른 문으로 선택을 바꾸든 자동차가 당첨될 확률은 각각 1/2로 동일하기에 굳이 선택을 바꿀 필요가 없을 것으로 보입니다.
다른 문으로 선택을 바꾼 것에 대한 벤의 설명은 다음과 같습니다. 처음에 3개의 문이 주어졌을 때 자동차가 당첨될 확률은 각각 1/3입니다. 하지만 사회자가 꽝인 문 하나를 열어 주었고, 다시 한 번 선택을 할 수 있는 상황에서 자신의 선택을 바꾼다면 당첨 확률이 2/3로 처음의 1/3보다 2배 상승하게 되니, 벤은 미키 교수에게 당첨 확률 1/3을 더 얹어 주셔서 고맙다는 인사와 함께 선택을 바꾸겠다고 한 것입니다.
미키 교수는 벤의 설명이 정확하다고 칭찬하며 부연 설명을 합니다. 보통 사람들의 경우 동일한 상황에서 추가적인 선택의 기회가 주어지면 대부분 자신의 선택을 변경하지 않는다고 합니다. 불신이나 두려움 따위의 감정 때문이라고 하면서 말이죠. 실제로 대다수의 사람들은 위와 같이 변화된 상황을 꽝이었던 하나가 제껴짐으로써 남은 두 개의 문 중에서 하나가 당첨될 수 있는 것이니 어느 것을 고르든 당첨 확률은 1/2이 될 것이고, 그나마 1/3에서 상승한 것으로 받아들이며, 여기에서 더 나아가 새로운 선택을 종용하는 사회자에 대한 불신 혹은 선택을 바꾸는 것에 대한 두려움으로 인해 굳이 선택을 바꾸지 않으려 한다는 것입니다. 심리학의 '인지 부조화 이론'에서 사람들은 자신의 선택을 정당화하고자 하는 성향이 있다고 설명하는 것처럼 말이죠.
여기까지 설명만으로는 대다수의 분들이 고개를 갸우뚱하실 겁니다. 사회자가 세 개의 문 중 꽝인 하나의 문을 열어줌으로써 두 개의 문 중 하나가 당첨되는 상황으로 바뀐 것인데, 선택을 바꿀 경우의 당첨 확률이 왜 1/2이 아니라 2/3가 되는 것인지 헷갈리실 테니까요. 그리고 영화를 보는 도중 이런 의문이 들기 시작하면 영화를 보는 내내 이 문제로 고민하게 되고, 영화에 집중하지 못 하는 사태가 발생할 수도 있습니다. 그러니 <21>을 보기 전에 왜 이렇게 되는 것인지를 미리 숙지하고 계신다면 저처럼 영화 내내 이 문제를 풀기 위해 고민하지 않으셔도 되지 않을까 싶어 간단하게나마 알려드리고자 이 글을 작성합니다.
수학자들조차 풀지 못 했던 '몬티홀 딜레마'
사실 이 문제는 '몬티홀 딜레마'라고 불리우는 매우 유명한 퀴즈입니다. 이 딜레마를 해결하기 위해 인터넷에서 검색을 통해 찾아보니 영화 <21>의 주인공인 벤 정도의 재능과 지식을 갖춘 사람이라면 이미 이와 관련된 자세한 내용을 알고 있었기에(영화의 배경이 된 시기가 1994년에서 1998년이고, 몬티홀 딜레마 문제가 널리 알려진 것이 1991년의 일이니까 말이죠.) 강의시간에 갑자기 출제된 문제를 풀 수 있지 않았을까 싶을 정도로 유명한 문제인 듯 하더군요.
미국의 쇼 프로그램인 "Let's Make a Deal"에서 유래된 문제로 이 프로그램의 진행자 이름이 몬티홀이었던 관계로 '몬티홀 딜레마'라는 이름이 붙게 된 것이라 합니다. 이러한 상황에 직면했을 때 어떻게 대처해야 할 지 궁금했던 사람들 중 한 명이 기네스북 최고의 IQ 보유자(IQ가 228이라고 합니다.)인 매릴린 사반트(Marilyn vos Savant)에게 해답을 구했고, 그녀는 1990년 9월 '퍼레이드'라는 잡지의 칼럼 '매릴린에게 물어보세요'에서 다음과 같이 충고했다고 합니다.
영화 <21>에서 벤의 답변과 동일한 내용입니다. 하지만 이러한 설명만으로는 여전히 의구심이 풀리지 않는 것이 당연합니다. 저만 의구심이 풀리지 않았던 건가요? ^^; 실제로 이와 같은 내용의 칼럼이 공개되고 나서 매릴린 사반트는 수학자들이 포함된 일련의 독자들로부터 엄청난 항의 서한을 받았다고 합니다. 그 항의 내용이란, 위 문제를 처음 접한 보통의 사람들이 생각하는 것처럼 처음의 선택을 바꾸든 바꾸지 않든 당첨될 확률은 각각 1/2로 동일하기 때문에, 선택을 바꾼다고 해서 당첨될 확률이 2/3로 상승할 수 없다는 내용이었습니다.
심지어 1996년에 돌아가신 정수론의 대가 폴 에어디쉬라는 유명한 수학자도 이 문제를 한 번 보고는 "나는 선택을 바꾸는 것만으로 확률이 달라진다는 사실에 동의할 수 없어. 다른 문으로 옮기든 원래 문을 고집하든 확률은 똑같을 테니까..."라고 고집을 피웠다고 하니, 대다수의 사람들이 어떻게 생각할지는 자명한 일일 것입니다. 물론 '이렇게 유명한 수학자들조차 선택을 바꾸든 바꾸지 않든 확률은 동일하다라고 했으니 그들의 말이 맞을 것야'라고 믿는 것이 전형적인 '권위에 호소하는 오류'를 범하는 꼴이 되어 버렸지만 말이죠. ^^
이러한 반박에 직면한 매릴린은 12월의 새로운 칼럼에서 수학 박사들의 혹독한 반박문을 게재한 뒤, 몬티홀 딜레마에 직면했을 경우 일어날 수 있는 가능한 6가지의 상황을 표로 제시하면서 반격했습니다. 그럼에도 논란은 그치지 않았고, 그녀는 1991년 2월 17일자 칼럼을 통해 세번째로 이 문제를 언급하였습니다. 나중에 어떤 수학자가 컴퓨터를 이용해 몬티홀 딜레마를 시뮬레이션화해 여러 차례 게임을 반복한 결과, 선택을 바꾸는 경우의 당첨 확률과 선택을 바꾸지 않는 경우의 당첨 확률의 비가 2:1로 나타났다고 합니다. 사반트, 그리고 영화 <21>에서 벤이 답변한 것처럼 선택을 바꿀 경우의 당첨 확률이 2/3, 선택을 바꾸지 않을 경우의 당첨 확률이 1/3이니 이 두 경우의 비가 2:1인 것과 정확하게 동일한 결과임을 입증한 것이죠.
정말로 선택을 변경하는 것이 유리할까?
실제로 몬티홀 딜레마와 같은 상황에 직면했을 때 위와 같은 결과가 나오는지 궁금하신 분들은 간단한 방법으로 동일한 상황을 경험해 보실 수 있습니다. 아래 링크를 클릭하시면 '몬티홀 딜레마'에서와 동일한 상황에 직면할 수 있으니까요. 시간이 많으시다면 직접 카드를 골라가면서 한 게임씩 시행해 보셔도 되고, 시간이 없으시다면 아래의 자동 실행 프로그램을 돌리셔도 상관 없습니다.
게임 횟수가 유한하기 때문에 앞에서 말씀드린 것처럼 선택을 변경할 경우 당첨 확률이 정확하게 66.7%가 나오지 않을 수는 있겠습니다만, 아마 그 비슷한 값이 나올 것입니다. '대수의 법칙'에 의해 게임 시도 횟수를 무한번으로 확장한한다면 선택을 변경할 경우 당첨 확률이 66.7%로 수렴하게 되겠죠. 어쨌든 위 웹페이지에서의 결과만 봐도 선택을 바꿀 경우의 당첨 확률이 2/3, 선택을 바꾸지 않을 경우의 당첨 확률이 1/3로 두 경우의 비가 2:1과 비슷하게 나온다는 것을 확인하실 수 있다는 겁니다.
왜 선택을 변경할 때의 당첨 확률이 2/3가 되는 것일까?
먼저 모든 경우의 수를 고려하는 방식으로 '몬티홀 딜레마'를 해결해 보도록 하겠습니다. 편의상 세 개의 문은 1번, 2번, 3번이라 하고 이 중 1번의 문에 자동차가 숨어 있다고 가정합니다. (나머지 2번 문이 당첨일 경우, 3번 문이 당첨일 경우도 이와 동일한 구조로 반복하시면 됩니다.) 이제 게임 속 주인공이 되어 한 개의 문을 선택하도록 해 보죠. 이 경우 게임에서 발생할 수 있는 모든 경우의 수는 다음과 같습니다. 매릴린 사반트가 제시했다는 도표가 아마도 이러한 경우의 수를 도표화한 것이 아닐까 싶습니다. 자료를 찾아보지 않아서 확언할 수는 없지만요. ^^;
처음에 1번 문을 선택했을 경우
기존 선택을 고수하면 -> 당첨, 기존 선택을 변경하면 -> 꽝
처음에 2번 문을 선택했을 경우
기존 선택을 고수하면 -> 꽝, 기존 선택을 변경하면 -> 당첨
처음에 3번 문을 선택했을 경우
기존 선택을 고수하면 -> 꽝, 기존 선택을 변경하면 -> 당첨
즉, 기존 선택을 고수했을 경우 당첨될 확률은 3가지 경우 중 처음 선택이 맞았을 경우 뿐이므로 이 때의 조건부 확률은 1/3이 됩니다. 하지만 기존 선택을 변경했을 경우 당첨될 확률은 3가지 경우 중 처음 선택이 틀렸을 2가지 경우를 모두 포함하므로 이 때의 조건부 확률은 2/3이 되는 것이죠.
이해를 쉽게 하기 위해 기존 선택을 고수하는 경우를 논외로 하고 무조건 선택을 변경하는 전략을 사용한다고 가정해 보도록 하겠습니다. 처음에 1/3의 확률로 당첨될 문을 골랐을 때 전략대로 자신의 선택을 변경한다면 꽝이 될 것입니다. 반면 2/3의 확률로 꽝인 문을 골랐을 때 전략대로 자신의 선택을 변경한다면 당첨될 것이구요. 즉, 자신의 선택을 변경하는 전략을 사용할 경우 2/3의 확률로 당첨될 수 있다는 결과를 도출할 수 있는 것입니다.
이번에는 자신의 선택을 변경하는 경우를 논외로 하고 무조건 자신의 선택을 고수하는 전략을 사용한다고 가정해 보도록 하겠습니다. 처음에 1/3의 확률로 당첨된 문을 골랐을 때 전략대로 자신의 선택을 고수한다면 당첨될 것입니다. 반면 2/3의 확률로 꽝인 문을 골랐을 때 전략대로 자신의 선택을 고수한다면 꽝이 될 것이구요. 즉, 자신의 선택을 고수하는 전략을 사용할 경우 당첨될 확률은 여전히 처음 세 개의 문이 주어졌을 경우와 다름없이 1/3에 불과하다는 결과를 도출할 수 있습니다.
몬티홀 딜레마와 동일한 논리 구조의 또 다른 문제
분명 처음 선택을 변경할 경우의 당첨 확률이 2/3로 처음 선택을 고수할 경우의 당첨 확률인 1/3보다 2배 더 높습니다. 하지만 왜 이런 결과가 나오는지에 대해서는 여전히 헷갈릴 수 있다고 생각합니다. 저 역시 한참을 헤맸으니까요. 뭐, 제가 헤맸으니 당연히 다른 분들도 헤매는 것이 정상이라고 말씀드리는 것은 아니구요. ^^; 이 몬티홀 딜레마를 좀 더 쉽게 이해하기 위해 동일한 논리 구조의 게임으로 치환해 보도록 하겠습니다.
몬티홀 딜레마와 동일한 논리 구조의 문제로의 치환 1
1번, 2번 3번 세 개의 문 중에서 게임 속 주인공인 여러분이 아무 것이나 문 하나(편의상 1번이라고 가정하겠습니다.)를 선택했습니다. 그러자 사회자 몬티홀이 새로운 제안을 합니다. 처음 선택했던 1번 문을 열어 볼 것인지, 아니면 선택하지 않았던 나머지 문 2개를 열어 볼 것인지 말이죠. 좀 더 쉬운 문제로 바꿔볼까요?
몬티홀 딜레마와 동일한 논리 구조의 문제로의 치환 2
1번, 2번, 3번 세 개의 문 중에서 게임 속 주인공인 여러분이 아무 것이나 문 하나(마찬가지로 편의상 1번이라고 가정하겠습니다.)를 선택했습니다. 그랬더니 사회자 몬티홀이 새로운 제안을 합니다. 처음 선택했던 1번 문을 열어 볼 것인지, 아니면 선택하지 않았던 나머지 문 2개를 열어 볼 것인지 말이죠. 그래서 도대체 사회자의 의도가 무엇일까 열심히 머리 굴려가며 생각하고 있을 무렵, 미처 결정하기도 전에 사회자가 처음 선택하지 않았던 2개의 문 중에서 하나를 열어 염소를 보여 줍니다.
위 2개의 문제는 몬티홀 딜레마와 논리 구조에서 전혀 다를 바가 없습니다. 자, 여러분이 게임 속 주인공이라면 어떤 선택을 하시겠습니까? 당연히 처음에 선택하지 않았던 나머지 문 2개를 열어보는 것으로 최초 선택을 변경해야 할 것입니다. 처음 선택했던 문을 고수한다면 당첨 확률이 1/3이지만, 선택을 변경해 나머지 2개의 문을 열어볼 수 있다면 당첨 확률이 2/3로 증가할 테니까요. 그리고 여러분이 선택을 변경할 것인지 말 것인지 미처 결정하기 전에 사회자가 나머지 2개의 문 중에서 염소가 숨어 있는 문 하나를 열어서 보여준다고 해도 선택을 변경할 경우의 당첨 확률이 2/3라는 사실에는 아무런 영향을 미치지 않기 때문에 그 경우에도 선택을 변경하는 것이 유리하다는 것은 자명합니다.
여러분이 처음에 선택하지 않았던 두 개의 문 중 사회자가 열지 않은 문, 즉 여러분이 선택을 변경할 경우 유일하게 선택할 수 있는 문이 당첨일 확률은 사회자가 두 개의 꽝인 문 중 하나를 오픈했을 때 1/3에서 2/3으로 바뀌게 됩니다. 자동차가 어디에 숨어 있는지 모르는 상황에서 여러분이 선택하지 않았던 두 개의 문 중에 하나가 당첨일 확률은 2/3입니다. 그런데 사회자가 친절하게도 두 개의 문 중에서 당첨이 아닌 한 개의 문을 제거해 줬습니다. 이 때 당첨이 아닌 한 개의 문을 제거한 사회자의 친절한 행동은 두 개의 문 중에 하나가 당첨일 확률값인 2/3에는 아무런 영향을 미치지 않습니다. 그러면 사회자가 제거하지 않았던 나머지 한 개의 문이 당첨일 확률은 당연히 2/3가 되는 것입니다.
그런데 이렇게 선택을 변경할 경우 당첨 확률이 증가한다는 사실을 직관적으로 받아들이지 못하는 이유는 무엇일까요? 심지어 수학자들조차도 헷갈릴 정도로 말이죠. 아마도 게임 속 주인공인 여러분이 한 개의 문을 선택하는 것과 사회자가 당첨이 아닌 한 개의 문을 열어서 보여주는 사건이 완전히 독립된 사건임을 쉽게 인식하지 못 했기 때문이 아닐까 싶습니다. 즉, 사회자가 꽝인 문 한 개를 열어주는 행위는 여러분이 선택했던 그 문의 당첨 확률에는 전혀 영향을 미치지 못 하는데도, 사람들은 보통 사회자의 행위가 여러분이 선택했던 문의 당첨 확률에까지 영향을 미쳐 나머지 두 개의 문 중 어떤 문을 선택하든 당첨 확률이 1/2로 증가하게 된다고 믿는 것이죠.
만약 몬티홀 딜레마 문제에서 순서를 약간 바꾸어 사회자가 염소가 있는 두 개의 문 중 한 개를 먼저 열어주고, 남은 두 개의 문 중 하나를 선택해야 할 경우의 당첨 확률은 1/2일 것입니다. 우리가 흔히 생각하는 것처럼 말이죠. 하지만 이러한 가정과 달리 몬티홀 딜레마에서는 여러분이 먼저 문을 선택한 후, 사회자가 염소가 숨어있는 문 한 개를 열어줍니다. 앞에서 설명했던 것처럼 염소가 숨어있는 문을 열어준 사회자의 행위는 여러분이 선택한 한 개의 문을 제외한 나머지 두 개의 문 사이에서만 발생합니다. 여러분이 처음에 선택했던 문의 당첨 확률인 1/3에는 전혀 영향을 미치지 않는다는 것입니다.
이러한 논리 구조를 따라가다 보면 결국 사회자는 여러분이 선택하지 않은 두 개의 문이 각각 가지고 있던 당첨 확률 1/3을, 꽝인 문 한 개를 열어줌으로써 여러분이 선택하지 않았던 나머지 한 개의 문에 옮겨다 줘 당첨 확률을 2/3으로 늘려준 셈이 된 것입니다. 그래서 영화 <21>의 주인공 벤이 교수님께 감사의 인사를 전했던 것이구요. ^^
의외로 간단한 문제인데도 설명을 하려니 무척이나 길어지는군요. 실제로 이 몬티홀 딜레마를 접하지 않은 상황에서 영화 <21>을 보게 된다면 미키 교수가 벤에게 제시한 문제를 풀기 위해 집착하느라 영화의 흐름을 놓칠 수도 있습니다. 실제로 저도 그랬구요. 혹시라도 영화 <21>을 보려고 계획하신 분은 이 몬티홀 문제를 미리 숙지해 놓은 상태에서 <21>을 보신다면 훨씬 더 재미있게 보실 수 있지 않을까 싶습니다. 물론 저와 다르게 영화를 보면서 바로 몬티홀 딜레마를 이해하실 수 있는 분도 계시겠지만요. ^^
혹시라도 현실에서 이와 비슷한 상황에 직면하는 경우가 발생한다면 먼저 몬티홀 딜레마와 동일한 구조가 맞는지 확인하시고, 무조건 자신의 선택을 변경하는 전략을 사용하시면 당첨 확률을 높일 수 있을 것입니다. 그것도 두 배나 높은 확률입니다. 이런 경우 선택을 바꾸는 것은 줏대없는 행동이 아니라 확률에 근거한 합리적인 행동인 것이니까 말이죠. ^^

영화의 기본 소재가 되는 MIT 수학 천재들의 라스베가스 원정기는 놀랍게도 1990년대 확률과 수학만으로 블랙잭의 법칙을 간파해 라스베가스를 제패한 '제프 마'의 실화에 바탕하고 있습니다. 이런 천재들의 실화에 바탕한 영화들을 볼 때면 '언젠가는 나도 저 천재들처럼 크게 한 탕...!!'이 아니고...-_-; 천재라 불리우는 사람들의 삶의 단면을 엿보는 듯한 즐거움을 느낄 수 있어 즐겨보곤 합니다. 이런 유형의 작품으로는 게임이론의 대가 '존 내쉬'의 이야기를 영화화한 '뷰티풀 마인드(Beautiful Mind)'가 있겠죠. '뷰티풀 마인드' 역시 참 재미있게 봤었는데, 예전에 봤던 영화라서 아직까지 후기를 못 쓰고 있네요. 언젠간 작성해야 하는데...^^;
아무튼 오늘의 포스팅은 영화 <21>에 대한 리뷰가 아니라 영화 <21>을 좀 더 편안하게 즐기기 위해 감상하기 전에 미리 알아두면 좋을 것 같은 포인트 하나를 알려드리기 위한 것입니다. 리뷰는 나중에 언젠가...-_- 혹시라도 영화를 봐야 하나, 말아야 하나 고민하고 계시는 분들을 위해 살짝 말씀드리자면...재밌습니다.

앞에서도 말씀드린 것처럼 미키 교수는 벤을 자신의 블랙잭 팀에 가입시키기 위해 꽤나 열심히 노력합니다. 미키 교수가 벤에게 호감을 가지기 시작한 시점은 바로 자신의 강의를 듣고 있던 벤의 뛰어난 수학 및 통계학 실력을 발견하고 나면서부터입니다.
강의 시간에 미키 교수가 '뉴턴의 공식'과 관련해 자신이 모르는 얘기를 좀 해 달라고 학생들에게 주문하자, 벤이 '뉴턴이 조셉 랩슨의 공식을 훔쳤다'라는 답변을 합니다. 벤의 답변에 흥미를 느낀 미키 교수는 벤에게 추가 점수를 얻을 수 있는 기회를 주겠다며 '게임 진행자의 문제'를 냅니다.
미키 교수가 제안한 '게임 진행자의 문제'
미키 교수가 제안한 '게임 진행자의 문제'는 다음과 같습니다. 벤이 게임쇼에 출연했다고 가정을 합니다. 세 개의 문 중에서 하나를 고르면 되는데, 한 개의 문 뒤에는 새로운 자동차가 기다리고 있고 나머지 두 개의 문 뒤에는 염소가 기다리고 있습니다. 이 중에서 새로운 자동차가 숨어 있는 문을 고르면 그 자동차를 선물로 얻을 수 있는 그런 게임입니다. 벤에게 어떤 문을 고르겠냐고 물어보는 미키 교수. 벤은 망설임없이 1번 문을 선택합니다.
벤의 선택을 듣고 난 교수는 추가적으로 새로운 정보를 제시합니다. 게임을 진행하는 사회자는 문 뒤에 무엇이 있는지 정확히 알고 있습니다. 그래서 벤이 고르지 않은 두 개의 문 중에서 하나의 문을 열어 제꼈더니 그 문 뒤에는 염소가 있었습니다. 일부러 염소가 숨어 있던 문을 선택해 열어준 것이죠.
이제 사회자는 벤에게 다가와 다시 한 번 선택을 하도록 제안합니다. 처음 선택한 1번 문을 그대로 선택할 것인지, 아니면 다른 문으로 바꿀 것인지 말이죠. 교수의 새로운 질문에 대해 벤은 또 다시 주저하지 않고 '바꾸겠다'라고 답을 합니다. 심리적인 문제에 근거한 것이 아니라 통계학에 근거하여 답한 것이라 설명하면서요. 벤이 선택을 바꾼 이유를 논리적으로 설명하고 나자 미키 교수는 벤에게 완전히 빠져들고, 벤을 자신의 블랙잭 팀에 가입시켜야겠다고 결심하게 됩니다.
자, 그런데 벤이 1번 문에서 다른 문으로 선택을 바꾼 것은 정말 통계학에 근거한 것일까요? 얼핏 생각하면 한 개의 문은 이미 꽝인 것으로 판명되었고, 나머지 두 개의 문 중에서 1개를 선택하는 것이므로 자신이 선택했던 1번 문을 그대로 선택하든, 다른 문으로 선택을 바꾸든 자동차가 당첨될 확률은 각각 1/2로 동일하기에 굳이 선택을 바꿀 필요가 없을 것으로 보입니다.
다른 문으로 선택을 바꾼 것에 대한 벤의 설명은 다음과 같습니다. 처음에 3개의 문이 주어졌을 때 자동차가 당첨될 확률은 각각 1/3입니다. 하지만 사회자가 꽝인 문 하나를 열어 주었고, 다시 한 번 선택을 할 수 있는 상황에서 자신의 선택을 바꾼다면 당첨 확률이 2/3로 처음의 1/3보다 2배 상승하게 되니, 벤은 미키 교수에게 당첨 확률 1/3을 더 얹어 주셔서 고맙다는 인사와 함께 선택을 바꾸겠다고 한 것입니다.
미키 교수는 벤의 설명이 정확하다고 칭찬하며 부연 설명을 합니다. 보통 사람들의 경우 동일한 상황에서 추가적인 선택의 기회가 주어지면 대부분 자신의 선택을 변경하지 않는다고 합니다. 불신이나 두려움 따위의 감정 때문이라고 하면서 말이죠. 실제로 대다수의 사람들은 위와 같이 변화된 상황을 꽝이었던 하나가 제껴짐으로써 남은 두 개의 문 중에서 하나가 당첨될 수 있는 것이니 어느 것을 고르든 당첨 확률은 1/2이 될 것이고, 그나마 1/3에서 상승한 것으로 받아들이며, 여기에서 더 나아가 새로운 선택을 종용하는 사회자에 대한 불신 혹은 선택을 바꾸는 것에 대한 두려움으로 인해 굳이 선택을 바꾸지 않으려 한다는 것입니다. 심리학의 '인지 부조화 이론'에서 사람들은 자신의 선택을 정당화하고자 하는 성향이 있다고 설명하는 것처럼 말이죠.
여기까지 설명만으로는 대다수의 분들이 고개를 갸우뚱하실 겁니다. 사회자가 세 개의 문 중 꽝인 하나의 문을 열어줌으로써 두 개의 문 중 하나가 당첨되는 상황으로 바뀐 것인데, 선택을 바꿀 경우의 당첨 확률이 왜 1/2이 아니라 2/3가 되는 것인지 헷갈리실 테니까요. 그리고 영화를 보는 도중 이런 의문이 들기 시작하면 영화를 보는 내내 이 문제로 고민하게 되고, 영화에 집중하지 못 하는 사태가 발생할 수도 있습니다. 그러니 <21>을 보기 전에 왜 이렇게 되는 것인지를 미리 숙지하고 계신다면 저처럼 영화 내내 이 문제를 풀기 위해 고민하지 않으셔도 되지 않을까 싶어 간단하게나마 알려드리고자 이 글을 작성합니다.
수학자들조차 풀지 못 했던 '몬티홀 딜레마'
사실 이 문제는 '몬티홀 딜레마'라고 불리우는 매우 유명한 퀴즈입니다. 이 딜레마를 해결하기 위해 인터넷에서 검색을 통해 찾아보니 영화 <21>의 주인공인 벤 정도의 재능과 지식을 갖춘 사람이라면 이미 이와 관련된 자세한 내용을 알고 있었기에(영화의 배경이 된 시기가 1994년에서 1998년이고, 몬티홀 딜레마 문제가 널리 알려진 것이 1991년의 일이니까 말이죠.) 강의시간에 갑자기 출제된 문제를 풀 수 있지 않았을까 싶을 정도로 유명한 문제인 듯 하더군요.
미국의 쇼 프로그램인 "Let's Make a Deal"에서 유래된 문제로 이 프로그램의 진행자 이름이 몬티홀이었던 관계로 '몬티홀 딜레마'라는 이름이 붙게 된 것이라 합니다. 이러한 상황에 직면했을 때 어떻게 대처해야 할 지 궁금했던 사람들 중 한 명이 기네스북 최고의 IQ 보유자(IQ가 228이라고 합니다.)인 매릴린 사반트(Marilyn vos Savant)에게 해답을 구했고, 그녀는 1990년 9월 '퍼레이드'라는 잡지의 칼럼 '매릴린에게 물어보세요'에서 다음과 같이 충고했다고 합니다.
"자동차를 받고 싶다면 선택을 바꾸는 것이 2배로 유리합니다.
처음의 선택을 바꾸지 않는다면 당첨될 확률이 1/3이지만,
다른 문으로 선택을 바꾸면 당첨될 확률이 1/3의 2배인 2/3이 됩니다"
처음의 선택을 바꾸지 않는다면 당첨될 확률이 1/3이지만,
다른 문으로 선택을 바꾸면 당첨될 확률이 1/3의 2배인 2/3이 됩니다"
영화 <21>에서 벤의 답변과 동일한 내용입니다. 하지만 이러한 설명만으로는 여전히 의구심이 풀리지 않는 것이 당연합니다. 저만 의구심이 풀리지 않았던 건가요? ^^; 실제로 이와 같은 내용의 칼럼이 공개되고 나서 매릴린 사반트는 수학자들이 포함된 일련의 독자들로부터 엄청난 항의 서한을 받았다고 합니다. 그 항의 내용이란, 위 문제를 처음 접한 보통의 사람들이 생각하는 것처럼 처음의 선택을 바꾸든 바꾸지 않든 당첨될 확률은 각각 1/2로 동일하기 때문에, 선택을 바꾼다고 해서 당첨될 확률이 2/3로 상승할 수 없다는 내용이었습니다.
심지어 1996년에 돌아가신 정수론의 대가 폴 에어디쉬라는 유명한 수학자도 이 문제를 한 번 보고는 "나는 선택을 바꾸는 것만으로 확률이 달라진다는 사실에 동의할 수 없어. 다른 문으로 옮기든 원래 문을 고집하든 확률은 똑같을 테니까..."라고 고집을 피웠다고 하니, 대다수의 사람들이 어떻게 생각할지는 자명한 일일 것입니다. 물론 '이렇게 유명한 수학자들조차 선택을 바꾸든 바꾸지 않든 확률은 동일하다라고 했으니 그들의 말이 맞을 것야'라고 믿는 것이 전형적인 '권위에 호소하는 오류'를 범하는 꼴이 되어 버렸지만 말이죠. ^^
이러한 반박에 직면한 매릴린은 12월의 새로운 칼럼에서 수학 박사들의 혹독한 반박문을 게재한 뒤, 몬티홀 딜레마에 직면했을 경우 일어날 수 있는 가능한 6가지의 상황을 표로 제시하면서 반격했습니다. 그럼에도 논란은 그치지 않았고, 그녀는 1991년 2월 17일자 칼럼을 통해 세번째로 이 문제를 언급하였습니다. 나중에 어떤 수학자가 컴퓨터를 이용해 몬티홀 딜레마를 시뮬레이션화해 여러 차례 게임을 반복한 결과, 선택을 바꾸는 경우의 당첨 확률과 선택을 바꾸지 않는 경우의 당첨 확률의 비가 2:1로 나타났다고 합니다. 사반트, 그리고 영화 <21>에서 벤이 답변한 것처럼 선택을 바꿀 경우의 당첨 확률이 2/3, 선택을 바꾸지 않을 경우의 당첨 확률이 1/3이니 이 두 경우의 비가 2:1인 것과 정확하게 동일한 결과임을 입증한 것이죠.
정말로 선택을 변경하는 것이 유리할까?
실제로 몬티홀 딜레마와 같은 상황에 직면했을 때 위와 같은 결과가 나오는지 궁금하신 분들은 간단한 방법으로 동일한 상황을 경험해 보실 수 있습니다. 아래 링크를 클릭하시면 '몬티홀 딜레마'에서와 동일한 상황에 직면할 수 있으니까요. 시간이 많으시다면 직접 카드를 골라가면서 한 게임씩 시행해 보셔도 되고, 시간이 없으시다면 아래의 자동 실행 프로그램을 돌리셔도 상관 없습니다.
'몬티홀 딜레마' 체험하러 가기
http://www.grand-illusions.com/simulator/montysim.htm
http://www.grand-illusions.com/simulator/montysim.htm
게임 횟수가 유한하기 때문에 앞에서 말씀드린 것처럼 선택을 변경할 경우 당첨 확률이 정확하게 66.7%가 나오지 않을 수는 있겠습니다만, 아마 그 비슷한 값이 나올 것입니다. '대수의 법칙'에 의해 게임 시도 횟수를 무한번으로 확장한한다면 선택을 변경할 경우 당첨 확률이 66.7%로 수렴하게 되겠죠. 어쨌든 위 웹페이지에서의 결과만 봐도 선택을 바꿀 경우의 당첨 확률이 2/3, 선택을 바꾸지 않을 경우의 당첨 확률이 1/3로 두 경우의 비가 2:1과 비슷하게 나온다는 것을 확인하실 수 있다는 겁니다.
왜 선택을 변경할 때의 당첨 확률이 2/3가 되는 것일까?
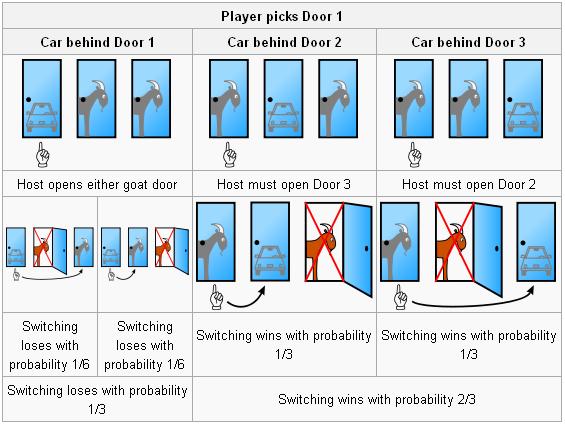
먼저 모든 경우의 수를 고려하는 방식으로 '몬티홀 딜레마'를 해결해 보도록 하겠습니다. 편의상 세 개의 문은 1번, 2번, 3번이라 하고 이 중 1번의 문에 자동차가 숨어 있다고 가정합니다. (나머지 2번 문이 당첨일 경우, 3번 문이 당첨일 경우도 이와 동일한 구조로 반복하시면 됩니다.) 이제 게임 속 주인공이 되어 한 개의 문을 선택하도록 해 보죠. 이 경우 게임에서 발생할 수 있는 모든 경우의 수는 다음과 같습니다. 매릴린 사반트가 제시했다는 도표가 아마도 이러한 경우의 수를 도표화한 것이 아닐까 싶습니다. 자료를 찾아보지 않아서 확언할 수는 없지만요. ^^;
처음에 1번 문을 선택했을 경우
기존 선택을 고수하면 -> 당첨, 기존 선택을 변경하면 -> 꽝
처음에 2번 문을 선택했을 경우
기존 선택을 고수하면 -> 꽝, 기존 선택을 변경하면 -> 당첨
처음에 3번 문을 선택했을 경우
기존 선택을 고수하면 -> 꽝, 기존 선택을 변경하면 -> 당첨

(이미지 출처 : 위키피디아 Monty Hall Problem)
즉, 기존 선택을 고수했을 경우 당첨될 확률은 3가지 경우 중 처음 선택이 맞았을 경우 뿐이므로 이 때의 조건부 확률은 1/3이 됩니다. 하지만 기존 선택을 변경했을 경우 당첨될 확률은 3가지 경우 중 처음 선택이 틀렸을 2가지 경우를 모두 포함하므로 이 때의 조건부 확률은 2/3이 되는 것이죠.
이해를 쉽게 하기 위해 기존 선택을 고수하는 경우를 논외로 하고 무조건 선택을 변경하는 전략을 사용한다고 가정해 보도록 하겠습니다. 처음에 1/3의 확률로 당첨될 문을 골랐을 때 전략대로 자신의 선택을 변경한다면 꽝이 될 것입니다. 반면 2/3의 확률로 꽝인 문을 골랐을 때 전략대로 자신의 선택을 변경한다면 당첨될 것이구요. 즉, 자신의 선택을 변경하는 전략을 사용할 경우 2/3의 확률로 당첨될 수 있다는 결과를 도출할 수 있는 것입니다.
이번에는 자신의 선택을 변경하는 경우를 논외로 하고 무조건 자신의 선택을 고수하는 전략을 사용한다고 가정해 보도록 하겠습니다. 처음에 1/3의 확률로 당첨된 문을 골랐을 때 전략대로 자신의 선택을 고수한다면 당첨될 것입니다. 반면 2/3의 확률로 꽝인 문을 골랐을 때 전략대로 자신의 선택을 고수한다면 꽝이 될 것이구요. 즉, 자신의 선택을 고수하는 전략을 사용할 경우 당첨될 확률은 여전히 처음 세 개의 문이 주어졌을 경우와 다름없이 1/3에 불과하다는 결과를 도출할 수 있습니다.
몬티홀 딜레마와 동일한 논리 구조의 또 다른 문제
분명 처음 선택을 변경할 경우의 당첨 확률이 2/3로 처음 선택을 고수할 경우의 당첨 확률인 1/3보다 2배 더 높습니다. 하지만 왜 이런 결과가 나오는지에 대해서는 여전히 헷갈릴 수 있다고 생각합니다. 저 역시 한참을 헤맸으니까요. 뭐, 제가 헤맸으니 당연히 다른 분들도 헤매는 것이 정상이라고 말씀드리는 것은 아니구요. ^^; 이 몬티홀 딜레마를 좀 더 쉽게 이해하기 위해 동일한 논리 구조의 게임으로 치환해 보도록 하겠습니다.
몬티홀 딜레마와 동일한 논리 구조의 문제로의 치환 1
1번, 2번 3번 세 개의 문 중에서 게임 속 주인공인 여러분이 아무 것이나 문 하나(편의상 1번이라고 가정하겠습니다.)를 선택했습니다. 그러자 사회자 몬티홀이 새로운 제안을 합니다. 처음 선택했던 1번 문을 열어 볼 것인지, 아니면 선택하지 않았던 나머지 문 2개를 열어 볼 것인지 말이죠. 좀 더 쉬운 문제로 바꿔볼까요?
몬티홀 딜레마와 동일한 논리 구조의 문제로의 치환 2
1번, 2번, 3번 세 개의 문 중에서 게임 속 주인공인 여러분이 아무 것이나 문 하나(마찬가지로 편의상 1번이라고 가정하겠습니다.)를 선택했습니다. 그랬더니 사회자 몬티홀이 새로운 제안을 합니다. 처음 선택했던 1번 문을 열어 볼 것인지, 아니면 선택하지 않았던 나머지 문 2개를 열어 볼 것인지 말이죠. 그래서 도대체 사회자의 의도가 무엇일까 열심히 머리 굴려가며 생각하고 있을 무렵, 미처 결정하기도 전에 사회자가 처음 선택하지 않았던 2개의 문 중에서 하나를 열어 염소를 보여 줍니다.
위 2개의 문제는 몬티홀 딜레마와 논리 구조에서 전혀 다를 바가 없습니다. 자, 여러분이 게임 속 주인공이라면 어떤 선택을 하시겠습니까? 당연히 처음에 선택하지 않았던 나머지 문 2개를 열어보는 것으로 최초 선택을 변경해야 할 것입니다. 처음 선택했던 문을 고수한다면 당첨 확률이 1/3이지만, 선택을 변경해 나머지 2개의 문을 열어볼 수 있다면 당첨 확률이 2/3로 증가할 테니까요. 그리고 여러분이 선택을 변경할 것인지 말 것인지 미처 결정하기 전에 사회자가 나머지 2개의 문 중에서 염소가 숨어 있는 문 하나를 열어서 보여준다고 해도 선택을 변경할 경우의 당첨 확률이 2/3라는 사실에는 아무런 영향을 미치지 않기 때문에 그 경우에도 선택을 변경하는 것이 유리하다는 것은 자명합니다.
여러분이 처음에 선택하지 않았던 두 개의 문 중 사회자가 열지 않은 문, 즉 여러분이 선택을 변경할 경우 유일하게 선택할 수 있는 문이 당첨일 확률은 사회자가 두 개의 꽝인 문 중 하나를 오픈했을 때 1/3에서 2/3으로 바뀌게 됩니다. 자동차가 어디에 숨어 있는지 모르는 상황에서 여러분이 선택하지 않았던 두 개의 문 중에 하나가 당첨일 확률은 2/3입니다. 그런데 사회자가 친절하게도 두 개의 문 중에서 당첨이 아닌 한 개의 문을 제거해 줬습니다. 이 때 당첨이 아닌 한 개의 문을 제거한 사회자의 친절한 행동은 두 개의 문 중에 하나가 당첨일 확률값인 2/3에는 아무런 영향을 미치지 않습니다. 그러면 사회자가 제거하지 않았던 나머지 한 개의 문이 당첨일 확률은 당연히 2/3가 되는 것입니다.
그런데 이렇게 선택을 변경할 경우 당첨 확률이 증가한다는 사실을 직관적으로 받아들이지 못하는 이유는 무엇일까요? 심지어 수학자들조차도 헷갈릴 정도로 말이죠. 아마도 게임 속 주인공인 여러분이 한 개의 문을 선택하는 것과 사회자가 당첨이 아닌 한 개의 문을 열어서 보여주는 사건이 완전히 독립된 사건임을 쉽게 인식하지 못 했기 때문이 아닐까 싶습니다. 즉, 사회자가 꽝인 문 한 개를 열어주는 행위는 여러분이 선택했던 그 문의 당첨 확률에는 전혀 영향을 미치지 못 하는데도, 사람들은 보통 사회자의 행위가 여러분이 선택했던 문의 당첨 확률에까지 영향을 미쳐 나머지 두 개의 문 중 어떤 문을 선택하든 당첨 확률이 1/2로 증가하게 된다고 믿는 것이죠.
만약 몬티홀 딜레마 문제에서 순서를 약간 바꾸어 사회자가 염소가 있는 두 개의 문 중 한 개를 먼저 열어주고, 남은 두 개의 문 중 하나를 선택해야 할 경우의 당첨 확률은 1/2일 것입니다. 우리가 흔히 생각하는 것처럼 말이죠. 하지만 이러한 가정과 달리 몬티홀 딜레마에서는 여러분이 먼저 문을 선택한 후, 사회자가 염소가 숨어있는 문 한 개를 열어줍니다. 앞에서 설명했던 것처럼 염소가 숨어있는 문을 열어준 사회자의 행위는 여러분이 선택한 한 개의 문을 제외한 나머지 두 개의 문 사이에서만 발생합니다. 여러분이 처음에 선택했던 문의 당첨 확률인 1/3에는 전혀 영향을 미치지 않는다는 것입니다.
이러한 논리 구조를 따라가다 보면 결국 사회자는 여러분이 선택하지 않은 두 개의 문이 각각 가지고 있던 당첨 확률 1/3을, 꽝인 문 한 개를 열어줌으로써 여러분이 선택하지 않았던 나머지 한 개의 문에 옮겨다 줘 당첨 확률을 2/3으로 늘려준 셈이 된 것입니다. 그래서 영화 <21>의 주인공 벤이 교수님께 감사의 인사를 전했던 것이구요. ^^
의외로 간단한 문제인데도 설명을 하려니 무척이나 길어지는군요. 실제로 이 몬티홀 딜레마를 접하지 않은 상황에서 영화 <21>을 보게 된다면 미키 교수가 벤에게 제시한 문제를 풀기 위해 집착하느라 영화의 흐름을 놓칠 수도 있습니다. 실제로 저도 그랬구요. 혹시라도 영화 <21>을 보려고 계획하신 분은 이 몬티홀 문제를 미리 숙지해 놓은 상태에서 <21>을 보신다면 훨씬 더 재미있게 보실 수 있지 않을까 싶습니다. 물론 저와 다르게 영화를 보면서 바로 몬티홀 딜레마를 이해하실 수 있는 분도 계시겠지만요. ^^
혹시라도 현실에서 이와 비슷한 상황에 직면하는 경우가 발생한다면 먼저 몬티홀 딜레마와 동일한 구조가 맞는지 확인하시고, 무조건 자신의 선택을 변경하는 전략을 사용하시면 당첨 확률을 높일 수 있을 것입니다. 그것도 두 배나 높은 확률입니다. 이런 경우 선택을 바꾸는 것은 줏대없는 행동이 아니라 확률에 근거한 합리적인 행동인 것이니까 말이죠. ^^
반응형
'My Favorites > 맨큐만의 경제학' 카테고리의 다른 글
| 니콘 스피드라이트 SB-900 60개월 할부로 구입, 삼성카드 온라인세이브 서비스 ! (9) | 2009.01.29 |
|---|---|
| 인터넷 쇼핑의 필수품 삼성카드로 인터넷 최저가 구매에 도전해 보자 ! (3) | 2008.11.30 |
| 외환(달러화, 유로화, 엔화)도 중요한 투자 수단 중 하나입니다. (14) | 2008.10.29 |
| 공짜로 문화생활(영화,연극,뮤지컬)을 즐기는 여러 가지 방법들 ! (22) | 2008.09.29 |
| 로또 1등 당첨자가 9번 나온 곳에서 로또 구입하면 당첨 확률도 상승? (29) | 2008.08.03 |
| SKT 망내 할인 요금제, T끼리 T내는 요금제&T끼리 플러스 할인 요금제 (10) | 2008.07.14 |
| 맨큐만의 경제학 - 머리말 (10) | 2008.06.16 |



댓글